The Latter Again Is More Conductive to the Former What Does This Mean
- Express Letter of the alphabet
- Open up Admission
- Published:
Electrical electrical conductivity of the global ocean
Earth, Planets and Infinite volume 69, Article number:156 (2017) Cite this article
Abstract
The electric conductivity of the ocean is a fundamental parameter in the electrodynamics of the Earth System. This parameter is involved in a number of applications ranging from the scale of in situ bounding main menstruation meters, through extensions of traditional induction studies, and into quite new opportunities involving the remote sensing of sea flow and properties from space-borne magnetometers such as carried aboard the 3 satellites of the Swarm mission launched in 2013. Here, the first ocean electrical conductivity data set calculated directly from observed temperature and salinity measurements is provided. These data describe the globally gridded, three-dimensional mean conductivity as well as seasonal variations, and the statistics of spatial and seasonal variations are shown. This "climatology" data fix of body of water conductivity is offered equally a standard reference similar to the ocean temperature and salinity climatologies that have long been bachelor.
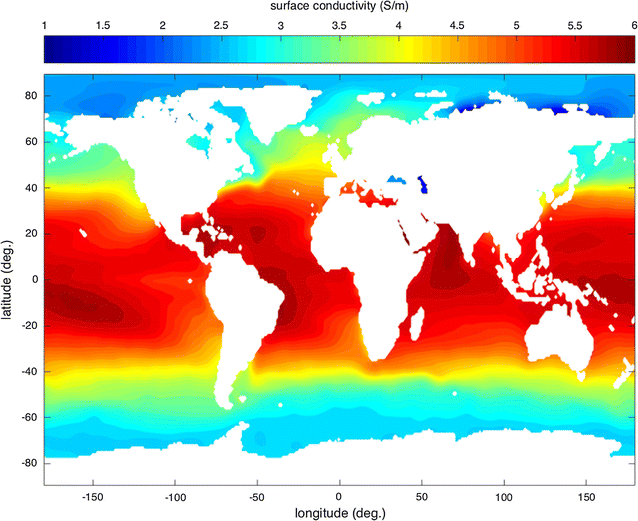
Introduction
The conductivity of the ocean is a fundamental parameter in the electrodynamics of the Earth System. It affects electrodynamic processes and the observable electromagnetic fields within the ocean merely also throughout the Earth's various components extending from the interior to the upper temper. Knowledge of the ocean'southward electrical conductivity is therefore required in studies of these processes and interpretation of these fields.
The electric conductivity referred to in this article is specifically the frequency-independent proportionality constant \(\sigma \) relating electrolytic conduction current density \({\mathbf {J}}\) to the electric field \({\mathbf {E}}'\) as measured in a frame moving with the fluid (the units of conductivity are Siemens/meter (i.e., S/m)). This relationship is expressed as Ohm's police force \({\mathbf {J}}=\sigma {\mathbf {E}}'\). Using the Lorentz transformation, this tin also exist written as \({\mathbf {J}}=\sigma \left( {\mathbf {East}}+{\mathbf {u}}\times {\mathbf {B}}\right) \), where \({\mathbf {E}}, {\mathbf {u}}\), and \({\mathbf {B}}\) are the electric field, fluid velocity, and magnetic field measured in the common rotating frame of the Earth. Maxwell's equations provide farther relationships to complete a closed set of equations from which general solutions tin be institute, only Ohm'southward police force alone establishes the importance of \(\sigma \) in opportunities attempting to infer components of \(\sigma , {\mathbf {J}}, {\mathbf {E}}, {\mathbf {u}}, {\mathbf {B}}\) from an incomplete set of observations.
A wide diversity of oceanographic instruments infer flow velocity from in situ measurements of the electrical field (see Tyler et al. 1997; Szuts 2012 for review material) or, more than accurately, the difference in electric potential between two points which, depending on the experimental blueprint, may exist separated by distances ranging from centimeters to hundreds of kilometers. The inference of flow from electric field measurements requires estimates of the electrical conductivity distributed over a region typically much larger than tin can be co-sampled in the same experiment with conductivity sensors. Hence, a database for accurately prescribing the conductivity distribution immediately improves the calibration of a wide variety of oceanographic period meters.
Since long, processes in the upper atmosphere and magnetosphere take been inferred from observed fluctuations in the geomagnetic field. Electric currents excited by dynamical processes in these regions cast magnetic fields reaching land and satellite magnetic observatories. Just these magnetic fluctuations too induce electric currents in the oceans and Globe, and so the observed magnetic fields are due to a combination of the primary and induced electric currents. Authentic inference of the processes in the upper temper and magnetosphere therefore depends on authentic cognition of the electrical conductivity distribution in the oceans and mantle.
Until relatively recently, most observations of the geomagnetic field were fabricated on state. Since 1999, even so, a number of long-term, low-orbit magnetic survey missions (Oersted, Gnaw, SAC-C) have provided unprecedented resolution, particularly over the oceans and other regions poorly covered by land observatories (e.1000., Olsen et al. 2006). In 2013, three depression-orbit satellites were launched in the showtime mission (Swarm, e.thou., Friis-Christensen et al. 2008) involving multiple infinite-borne magnetic observatories aimed to farther increase the detail in the observed magnetic fields. This new epoch of satellite magnetic surveys has opened new opportunities, some extending from the applications described above, and some quite novel. Many of these opportunities involve interpretation of large-calibration, relatively weak fluctuations in the Earth'southward magnetic field that in turn involve electric currents (either primary or induced) in the ocean (east.thou., run into Kuvshinov 2008 for review). Hence, much of the modern development in geomagnetic studies has go dependent on the accuracy in modeling oceanic electric currents, and the priority for improve agreement the distribution of electrical conductivity in the sea has risen.
In the following two subsections, the physics of body of water electric conductivity is described, and a description of the methods used in previous estimates of this parameter is given. The methodology of this study is presented in "Methodology" section, and the results are presented in "Climatology of bounding main electrical electrical conductivity" section. In "Use of climatology to assess errors in previous assumptions" section, a brief clarification of errors associated with previous conductivity estimates is provided, a discussion is included in "Decision" section, and information on obtaining the data is given in "Availability of data and materials" section. This data set of the long-term (1981–2010) climatological mean shall be referred to hither as the "climatology," consistent with nomenclature for other sea data.
Electrical conductivity of seawater
Within the parameters of Earth'south oceans, the electrical electrical conductivity of seawater depends on temperature, salinity, and to a much smaller caste pressure (depth). Salts such as sodium chloride (NaCl) disassociate in water to form cations (\(\hbox {Na}^{+}\)) and anions (\(\hbox {Cl}^{-}\)) that drift in the presence of an electric field, thereby producing an electric electric current. Information technology is then easy to empathize that the electrical conductivity \(\sigma \) increases with the concentration of dissolved salts (salinity Due south). The conductivity likewise increases with increasing temperature T, and this may be reasonably associated with an increase in mobility of the ions. Although the increment of \(\sigma \) with T and S may be hands understood intuitively, this does not immediately provide much indication of the distribution of \(\sigma \) in the body of water, fifty-fifty for oceanographers familiar with the distributions of T and S. Even the typical vertical profile of \(\sigma \) is not easily anticipated because of opposing tendencies in the dependencies of conductivity and density on T,Southward. While \(\sigma \) increases with both T and S, the water density \(\rho \) increases with S but decreases with T. With possible exceptions that are volumetrically rare (eastward.g., surf zones), the oceans are stably stratified and \(\rho \) increases with depth. This alone, however, does non immediately provide intuition on the profile of \(\sigma \) or whether the profile is even monotonic with depth. It seems then to be the case that quantitative and even qualitative understanding of the distribution of ocean electrical conductivity must exist obtained through original analyses of observations, rather than through reference to other well-described ocean parameters.
Global conductivity in previous studies
In early studies, and fifty-fifty continuing to contempo piece of work (east.thousand., Tyler et al. 2003; Kuvshinov et al. 2006; Schnepf et al. 2014; Sabaka et al. 2015), the electric conductivity of the ocean has often been assumed to exist uniform. In some applications involving idealized or model comparison studies, this may be justified but it is also articulate that a reliable global clarification or gridded data set of the observed sea conductivity was not available. Tyler et al. (1997) and several subsequent studies extending to the present (e.chiliad., Irrgang et al. 2016a, b) included a description of the iii-dimensional ocean conductivity as obtained from the temperature, salinity, and pressure variables in a global sea circulation model. While the electrical conductivity obtained this way is expected to be dynamically consequent, it remains unclear how realistic the clarification is and, well-nigh importantly, how well it agrees with the large gear up of scattered observations.
Climatology data sets for other ocean parameters (e.k., temperature, salinity, density) take long been available and used in a broad variety of oceanographic applications ranging from observational studies to ocean modeling. But a climatology data set for conductivity has not previously been available and construction of such requires a major try. Climatologies of ocean temperature and salinity, for example, attempt to correspond the nigh reliable gridded data sets that can be constructed from the large set up of historical observations taken using a variety of methods and instrumentation. Electrical conductivity depends nonlinearly on temperature and salinity, and the separate temperature/salinity climatologies are constructed from quite dissimilar sample distributions. Conductivity should then be calculated from co-observed temperature and salinity.
Alternatively, ane may calculate a description of electrical conductivity straight from climatologies of temperature and salinity. Such an approach was used to obtain the conductivity in Manoj et al. (2006), and these data have been adopted in later studies (eastward.one thousand., Kuvshinov 2008; Sabaka et al. 2015; Schnepf and Kuvshinov 2015; Grayver et al. 2016). While this may reasonably provide a quick approach to obtaining a gridded conductivity information gear up, a major weakness is that the realism is immediately suspect and the uncertainties are not easily assessed. The merely published study then far to include gridded conductivity calculated from observations is the Tyler tidal magnetic field simulation in Sabaka et al. (2016). The latter data (a preliminary data set of that presented in this study) used information from the longer range 1978–2012, and this date range was adapted to 1981–2010 in this study to follow the time bridge convention of other climatologies.
As described, previous descriptions of global ocean conductivity are either recognizably simplistic, or their degree of realism is difficult to appraise. Of form with the climatology provided hither, the errors associated with previous approaches tin at present be addressed, and a discussion toward this is included in "Use of climatology to assess errors in previous assumptions" department.
Methodology
In this department, the algorithm used for computing seawater electrical electrical conductivity from temperature, salinity, and pressure is first presented, and and then the information serving as input is described.
Algorithm for computing conductivity
The electric electrical conductivity (\(\sigma \)) of seawater became 1 of the fundamental oceanographic parameters in the 1950s with the increased apply of loftier-precision electrical conductivity bridges for salinity determinations. After near 70 years of using the dilution theory provided past Knudsen et al. (1902), the practical salinity (S) was defined on the Practical Salinity Scale of 1978 (PSS-78) in terms of the electrical conductivity ratio to the reference, and its relationship with \(\sigma \), temperature (\(t_{68}\), IPTS-68), and pressure (p, zero dbar at one atmospheric pressure) was incorporated in the Equation of State for Seawater (EOS-80; east.g., Fofonoff and Millard 1983; Fofonoff 1985). Although the international thermodynamic equation of seawater 2010 (TEOS-10; IOC et al. 2010) superseded EOS-lxxx, the relationship in EOS-eighty associated with the conductivity is yet valid. In this study, we use gsw_C_from_SP in the Gibbs Seawater (GSW) Oceanographic Toolbox (McDougal and Barker 2011; IOC et al. 2010) to calculate \(\sigma \) from S,p, and the temperature on ITS-90, T (TEOS-10 is used with no conversions between temperature scales; if information were in IPTS-68 or ITS-90, we used information technology directly). In both EOS-80 and TEOS-10, the electrical conductivity, \(\sigma \), is calculated using the relationship,
$$\begin{aligned} \sigma (South,t_{68},p)=\sigma (35,xv\,^{\circ }\mathrm{C},0\;\mathrm{dbar})\cdot R, \end{aligned}$$
(i)
where R is the solution of
$$\begin{aligned} r_{t}(t_{68})\cdot R_{t}\cdot \left( 1+\frac{C_{p}(p)}{A(t_{68})\cdot R+B(t_{68})}\right) -\,R=0, \end{aligned}$$
and \(R_{t}\) is obtained by solving the following equation:
$$\begin{aligned} \left\{ \sum _{i=0}^{5}\left( a_{i}+\frac{t_{68}-15}{1+one thousand(t_{68}-15)}b_{i}\right) (R_{t})^{i/2}\right\} -\,S=0. \terminate{aligned}$$
(2)
Here, \(r_{t}(t_{68})=\sum _{i=0}^{4}c_{i}t_{68}^{i}, B(t_{68})=ane+d_{1}t_{68}+d_{2}t_{68}^{2}, A(t_{68})=d_{iii}+d_{four}t_{68}\), and \(C_{p}(p)=e_{1}p+e_{ii}p^{2}+e_{iii}p^{3}\), while \(k, a_{i}, b_{i}, c_{i}, d_{1\ldots 4},\) and \(e_{1\ldots 3}\) are empirical coefficients.
The reference conductivity is \(\sigma (35,fifteen\,^{\circ }\mathrm{C},0\;\mathrm{dbar})=4.29140\) (Due south/thou). Between the ii temperature scales, IPTS-68 and ITS-90, T is linked to \(t_{68}\) by the relationship, \(t_{68}= one.00024 \cdot T\). While Eq. (1) is valid but in the range of \(2<S<42\), GSW Toolbox adopts the method of Colina et al. (1986) for the range of \(0<S<2\). Refer to Fofonoff (1985) and IOC et al. (2010) for more details about Eq. (ane).
Concurrent salinity, temperature, and pressure level measurements used to calculate electrical conductivity come up from the World Ocean Database (hereafter WOD). Descriptions of data sources for this drove of oceanographic profile data, instrumentation, temporal and spatial distributions, measurement accuracies, and quality control procedures can be plant in Boyer et al. (2013). Just concurrent salinity and temperature profiles taken during or afterwards 1981 were used for consistency in the definition of salinity (PSS-78). Pressure level was used when reported; otherwise, information technology was calculated from reported depth measurements. Although most salinity values in this time menses are derived from conductivity measurements, the conductivity was not usually reported, hence the need to dorsum calculate conductivity. The aforementioned procedures every bit outlined in Zweng et al. (2013) were followed to calculate objectively analyzed climatological hateful fields of conductivity for the period 1981–2010 at 102 standard depth levels from the surface to 5500 chiliad depth. Briefly, one-caste gridded hateful values of conductivity at each standard depth were compiled after back calculation, subject to quality control procedures. An objective analysis technique (Cressman 1959; Barnes 1964) was employed to modify each ane-degree mean based on the divergence between a first-approximate field and the compiled hateful of each one-degree square within a given radius of influence. The first-guess field for the annual (all-data) field was a bowl specific zonal average. The first-guess field for the four seasonal fields (Winter = January–March, etc.) was the annual climatological mean. The commencement-guess for each month was the appropriate seasonal climatological mean. Monthly fields only extend to 1500 m, as there is little annual wheel (and thin data) below that level. Annual and seasonal fields extend to 5500 chiliad depth.
Climatology of sea electrical conductivity
In this study, the temporal mean ocean conductivity data for the global body of water have been calculated following the method described in "Methodology" department. We keep here to describe characteristics of this data set which is bachelor at https://www.nodc.noaa.gov/OC5/woa13/.
The temporal mean conductivity \(\sigma =\sigma (\text{ longitude, } \text{ breadth, } {-\,z) }\) is a three-dimensional array, with each value representing a cell volume which varies with latitude and depth (\(-\,z\)). The volumetrically weighted mean conductivity of the global ocean is iii.31 ± 0.23 S/m.
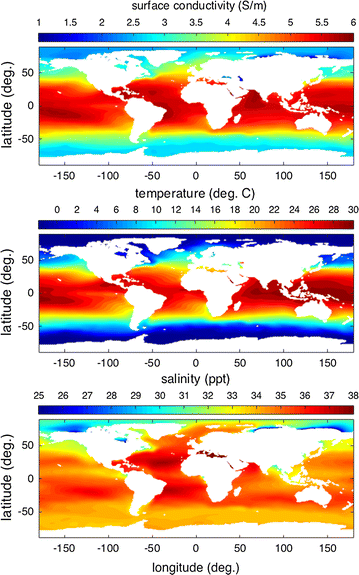
Electrical electrical conductivity, temperature, salinity, and density at the surface of the global ocean. The full ranges in the surface data are, respectively, 0.0999–vi.45 (Due south/m), − 1.84–30.half dozen (C), 5.02–forty.ane (ppt)
In Fig. 1, we see that the values and variability of the conductivity at the ocean surface are much larger than the volume quantities. In that location is a strong latitudinal variation that primarily tracks that of temperature. But in fresh inland seas and locations near the mouths of rivers, conductivity primarily depends on salinity. The salinity dependence is quite extreme in the Arctic considering the temperature is relatively abiding (almost freezing), there are many large rivers supplying freshwater, and alkali rejection/salt dilution during ice formation/melt makes the variability of salinity loftier. Because evaporation exceeds precipitation over the Mediterranean (and more often than not the Atlantic), both salinity and conductivity are elevated compared to other locations at similar temperatures.
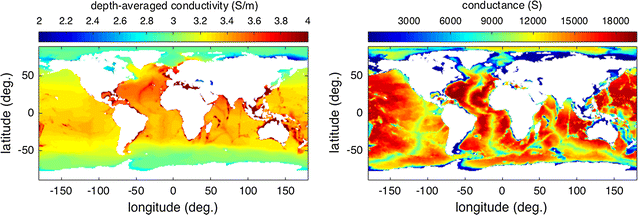
Depth-averaged electrical conductivity and conductance of the global ocean. The full range in the data is, respectively, 0.212–vi.36 (S/1000) and 0–1962 (S)
The depth-averaged conductivity is shown in Fig. 2. Away from warm, shallow areas and the freshwater of rivers and inland seas, i sees that the depth-averaged electrical conductivity is remarkably constant over near of the global body of water. This is an immediate indication that almost of the variability seen in Fig. 1 does not extend very deep into the body of water. The related depth integral (i.e., the depth-averaged electrical conductivity multiplied by the ocean depth) is referred to as the conductance (Due south) and is also shown in Fig. 2. The globally averaged profile of electrical conductivity with depth is shown in Fig. iii, together with similar profiles for T,S.
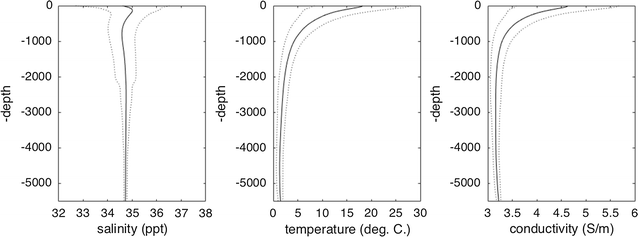
Globally averaged electrical conductivity profile with depth (profiles for temperature and salinity shown for comparison). Dash lines evidence the envelope of 1 standard deviation
To narrate the 3-dimensional beliefs of the electrical conductivity, nosotros follow an arroyo used in oceanography in which T,Due south are used as plotting coordinates. Because a h2o mass' T,S backdrop are primarily set past processes occurring at the sea surface, the T,S coordinates are often useful in identifying the location of origin of the water mass. In Fig. four, a besprinkle plot of the electrical conductivity data is shown using T,S (and depth, \(-\,z\)) every bit coordinates. The value of the conductivity \(\sigma \left( T,South,-\,z\correct) \) is shown past the colour scale. Several projections onto planar surfaces are included and used toward the following description.
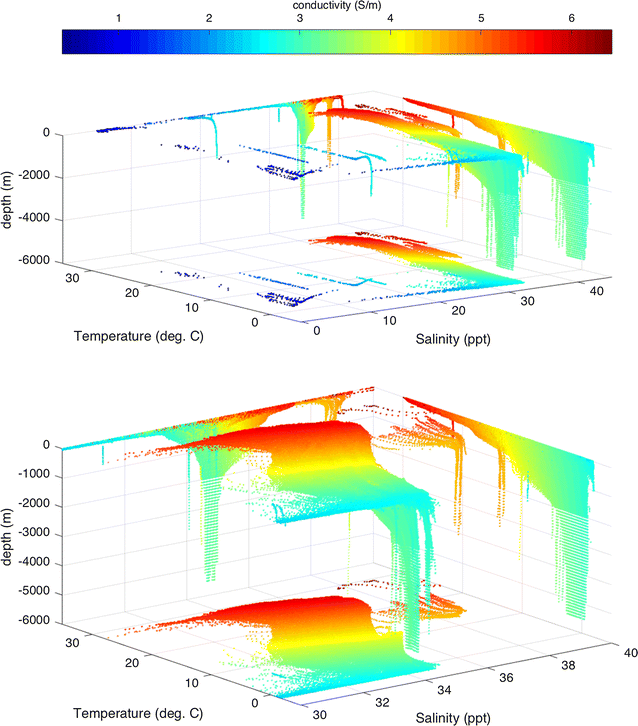
Scatter plot showing information gear up of global ocean conductivity (values given by color calibration) as distributed in coordinates of co-located salinity, temperature, and depth. Planar projections are also included. Clusters draw distinct water mass properties from diverse body of water bodies. The bottom panel is a magnification of the height panel, excluding the atypical low-salinity clusters associated with inland seas (run across text). Most of the variability is virtually the sea surface
Consider the projection onto the \(-\,z=6000\) grand surface (as seen in the superlative panel of Fig. iv). Several point clusters with low South coordinate correspond to inland seas (Caspian, Black, Baltic) and the Arctic. Excluding these regions, we magnify this figure (bottom panel) and run into that bated from a cluster with loftier T,Due south (the Mediterranean), nigh of the global bounding main conductivity is remarkably uniform at depth (see besides the Additional file 3 which shows a movie of electrical conductivity surfaces from the surface to seafloor).
Above, the spatial variability of the temporally averaged electrical conductivity has been described. At present we shall describe the temporal variability. One should annotation that even the time-averaged conductivity climatology can be useful in understanding and predicting temporal variability caused by fluid movement. Figures 3 and iv show that there are typically large vertical gradients near the surface. Therefore, vertical fluid motion (east.g., internal waves, convection) can cause temporal variability in the conductivity measured at a given location. Although the horizontal gradients in conductivity are much smaller than the vertical gradients, persistent advection by bounding main currents associated with eddies, waves, and tides tin also lead to important temporal fluctuations in conductivity. The expected amplitudes of these fluctuations depend very much on the features considered, but a simple guess is \(\Delta \sigma \sim |{\mathbf {u}}\cdot \nabla \sigma |\Delta t\) , where \(\Delta \sigma \) is the amplitude of the anomaly, \(|{\mathbf {u}}\cdot \nabla \sigma |\) is the aamplitude of the dot product of flow velocity \({\mathbf {u}}\) (which may consider vertical or horizontal components) and the gradient of the conductivity, and \(\Delta t\) is the time scale for the process. On the large scales relevant to the applications described in this article, the most predominant temporal fluctuation to look is due to the seasonal changes in the fluxes of estrus and freshwater across the ocean boundaries. For the purposes of the big-calibration climatology described here, we shall use the seasonal changes to characterize the temporal variability in the ocean's conductivity. In Fig. 5, the surface values are seen to vary \(\sim \,1\) Southward/g over the seasonal cycle, the fluctuations traceable to expected seasonal variations in heat and freshwater fluxes. The large-scale seasonal variations at the surface show, at mid and low latitudes, a ascendant dependence on hemispheric warming/cooling rather than salinity. Regionally (notably the Arctic) conductivity fluctuations can show strong dependence on river runoff.
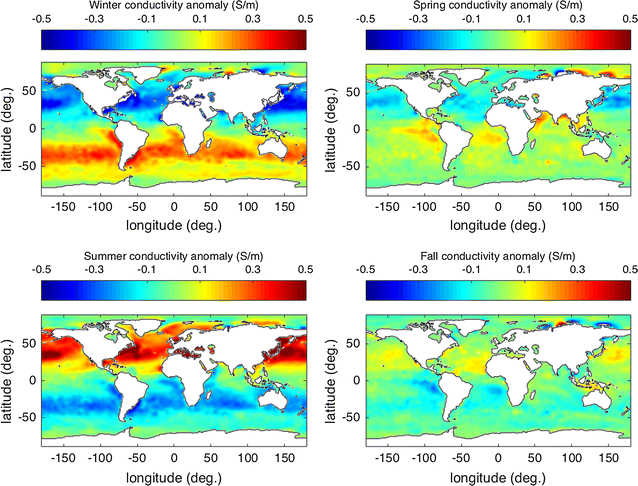
Ocean surface electrical conductivity anomaly (relative to almanac mean) for each of the four seasons. The full range in the data is for Winter, Spring, Summer, and Fall, respectively, − 0.852–0.520 (S/m), − 0.626–0.506 (S/m), − 0.633–0.963 (S/grand), and − 0.591–0.642 (S/m)
As shown in Boosted file 1: Fig. S1, we come across that the depth-averaged temporal fluctuations are typically extremely small \(\sim \,0.01\) S/m. The corresponding fluctuation in terms of conductance is \(\sim 50\) S. This is consequent with the expectation that most of the seasonal variations in the surface fluxes of heat and freshwater practice non penetrate below the tiptop few hundred meters of the ocean.
In that location are two sources of dubiousness to consider in the electrical conductivity climatologies. The climatological mean value is a unmarried value representing the mean over the given time period at each one-degree grid box. Still, in that location is variation around that mean, both natural variation and that caused past measurement uncertainty. The measurement accuracy for a standard Seabird 911+ CTD instrument is 0.00003 S/one thousand for conductivity and 0.001C for temperature. In practice, due to bounding main conditions, CTD calibration, and measurement procedures, the uncertainty in conductivity may be higher. Information technology is difficult to split natural variations from measurement uncertainty. So the standard error of the hateful represents the combined incertitude of the hateful value for each depth at each 1-degree filigree box. The global mean of the standard mistake is 0.02 S/k at the surface and 0.003 S/g at g m depth for monthly climatological mean fields and \(0.04 \pm 0.03\,\hbox {S/thousand}, 0.004 \pm 0.004\) Due south/m at the surface and thou m, respectively, for the annual climatological mean field. The annual mean field has a higher standard error, as expected, as it encompasses the entire seasonal cycle. The 2nd measure of incertitude is the difference between the observed mean and the objectively analyzed hateful at each one-degree grid box. This is a measure of the uncertainty introduced in the objective analysis procedure. It is not an contained measure from the standard fault of the mean, every bit the natural variations and discrepancies in measurement accuracy play a role in the differences between values in nearby filigree boxes and hence are partially responsible for the departure between observed and analyzed mean fields. For monthly fields at the surface, the global mean observed minus analyzed is approximately \(0.003 \pm 0.08\) S/m, while at k m the value is \(0.0004 \pm 0.02\) South/grand. For the annual time period at the surface, the global mean observed minus analyzed difference is \(0.006 \pm 0.09\) Southward/m at the surface and \(0.0005 \pm 0.01\) Due south/g. All values are for the 1981–2010 climatological mean fields of electrical conductivity. Full fields of standard fault of the mean and observed minus analyzed difference are provided with the climatological hateful fields of electrical conductivity at https://www.nodc.noaa.gov/OC5/woa13/.
Use of climatology to appraise errors in previous assumptions
As described in "Introduction" department, a weakness in previously assumed sea conductivity distributions was the difficulty in assessing the realism or associated errors in the estimates. With the climatology provided here, ane may now assess these errors. Although some comments and comparisons are included here, information technology should be noted that with the climatology information now available there is little reason to justify the connected apply of simplistic assumptions. The discussion here then serves only to address errors due to assumptions used in previous applications. As this is not the goal of this newspaper, the discussion here is kept cursory. Because accuracy in the previous applications can depend on not just the values of the conductivity but also the gradients and integrals, information technology is also clear that such an mistake assessment would remain incomplete unless performed by the original investigators using the new conductivity data provided.
Equally described in "Methodology" section, we calculated the gridded electrical conductivity information set up by start calculating conductivities from meantime measured in situ T,Southward,p and and then conducting the objective analysis against the irregularly distributed conductivity data. I can much more than easily obtain a gridded conductivity data set up by straight calculating electrical conductivity from existing T,S,p climatologies, as conducted in Manoj et al. (2006). However, the latter electrical conductivity data need non be representative nor fifty-fifty realistic.
The climatological T,S information in the World Ocean Atlas 2013 (Boyer et al. 2013; Zweng et al. 2013) correspond spatial/temporal distributions of observed T,S, but the distributions of observed T,S information are somewhat unlike because some observations reported simply one of either T or Southward. While climatologies of either T or S tin exist obtained through objective analyses of the respective T,Due south data available, problems can go far when 1 attempts to combine these data derived from different temporal/spatial distributions of original information. This is especially a concern in the case here where the calculation of conductivity involves a nonlinear dependence on T,S. The latter arroyo may indeed requite conductivity values that are neither representative nor realistic. At the heart of this matter is the fact that the formulae for calculating conductivity from T,S crave that the T,S measurements are taken at the same time and location. The approach in this study restores this requirement by creating conductivity climatologies from coincident, co-located T,Southward observations rather than the processed T,S climatological products.
Several previous studies treated the ocean equally having a compatible electrical conductivity of value 3.2 South/m (Tyler et al. 2003; Kuvshinov et al. 2006; Schnepf et al. 2014; Sabaka et al. 2015). This can exist compared with the global mean of iii.31 S/thousand described in "Climatology of body of water electrical conductivity" section. One also sees in Fig. 2 that supposition of a uniform value is quite crude as there are both regional and zonal departures. Almost notably, the Arctic, with its large river runoff, has much lower electrical conductivity due to the reduction in salinity, and a global-calibration reduction due to the lower temperatures at loftier latitudes is also credible.
While information technology can be immediately appreciated that the conductivity data presented here are significantly more realistic than the assumption of uniform ocean conductivity, the improvement over the data previously calculated from T,S climatologies is less immediate to describe and is therefore included in Boosted file 2: Supporting Data to this paper. In cursory, conductance calculated in the 2 methods (or fifty-fifty with the uniform conductivity supposition) appears very like over most of the ocean, but this is primarily merely reflecting the mutual ocean depth used in all cases. Test of the gradients of conductance and its inverse testify larger fractional differences in the methods. Finally, a better exam of the differences (in terms of testing the ocean conductivity distribution causeless rather than common integration limits) is in comparison the depth-averaged conductivity and its gradients (as shown in Additional file 3: Supporting Information). In this latter case, in that location are large differences between the 2 methods.
In summary, the results here back up idealized ocean electrical conductivity assumptions as an approximation (compatible conductivity multiplied past realistic ocean depth gives a reasonable conductance distribution, and one may even obtain a reasonable depth-averaged conductivity assuming a common electrical conductivity depth profile appropriately representing the global averaged behavior). The electrical conductivity distribution as calculated in Manoj et al. (2006) may similarly serve the same level of approximation but also shows spurious features such that it is recommended that use of these information is discontinued in favor of the data presented here in applications attempting to stand for the realistic electrical conductivity of the ocean.
Conclusion
The generation and analyses of the conductivity climatology data gear up have shown that the spatial and seasonal variability is remarkably small, at least when compared with the electrical conductivity in other components of the Earth System which may typically show orders of magnitude variations in both space and time. The ocean appears to be the only large-scale component of the Earth System with such highly anticipated electric conductivity, and the data presented hither provide a standard reference. This stability and predictability of the ocean conductivity is very important in a number of induction and motional induction applications where naturally occurring magnetic fields (driven by external fields or flow) may be used to infer period and electrical parameters in the ocean and solid Earth. In some case (due east.g., tides) where the forces ultimately driving oceanic electric currents are also highly predictable, the ocean may provide the near predictable naturally occurring large-scale sounding source on Globe. In this instance, the data presented here may exist used to quantify the stability of such sources.
While the electrical conductivity of the ocean may be more stable and anticipated than other components of the Globe Arrangement, the climatology presented also shows interesting spatial and temporal variations. Immediately credible are the effects of seasonal heating and river runoff.
Quantifying errors in by studies due to simplistic assumptions for the conductivity is necessarily incomplete equally accuracy can depend on not only the conductivity values used merely too the gradients and integrals. Some reassurance in past simplistic assumptions is provided here in that the spatial variability is seen to exist relatively minor and/or described by roughly like depth profiles (hence, arcadian assumptions are non every bit bad as they could first seem). But in attempting to represent more than realistic ocean conductivity, it is recommended that use of conductivity every bit calculated in Manoj et al. (2006) be discontinued in favor of the results provided hither. Hereafter studies that intentionally keep to use idealized or bounding main model conductivity distributions may also now draw from the statistics and data provided here.
References
-
Barnes SL (1964) A technique for maximizing details in numerical atmospheric condition map analysis. J Appl Meteorol iii(4):396–409
-
Boyer TP, Antonov JI, Baranova OK, Garcia HE, Johnson DR, Mishonov AV, O'Brien TD, Seidov D, Smolyar I, Zweng MM et al (2013) World Ocean Database 2013. In: Levitus S, Mishonov A (eds) Tech. Ed. NOAA Atlas NESDIS, vol 74
-
Cressman GP (1959) An operational objective analysis system. Mon Weather Rev 87(ten):367–374
-
Fofonoff NP, Millard RC (1983) Algorithms for ciphering of fundamental properties of seawater. UNESCO Technical Papers in Marine Science 44
-
Fofonoff NP (1985) Physical backdrop of seawater: a new salinity calibration and equation of state for seawater. J Geophys Res Oceans (1978–2012) xc(C2):3332–3342
-
Friis-Christensen E, Luhr H, Knudsen D (2008) Swarm—an World ascertainment mission investigating geospace. Adv Infinite Sci 41:210–216
-
Grayver AV, Schnepf NR, Kuvshinov AV, Sabaka TJ, Manoj C, Olsen Due north (2016) Satellite tidal magnetic signals constrain oceanic lithosphere–asthenosphere boundary. Sci Adv 2(9):e1600798. https://doi.org/10.1126/sciadv.1600798, http://advances.sciencemag.org/content/2/nine/e1600798
-
Colina KD, Dauphinee T, Wood DJ (1986) The extension of the practical salinity scale 1978 to depression salinities. IEEE J Body of water Eng 11(1):109–112
-
IOC, SOR, IAPSO (2010) The international thermodynamic equations of seawater-2010: calculation and use of thermodynamic properties. UNESCO
-
Irrgang C, Saynisch J, Thomas M (2016a) Ensemble simulations of the magnetic field induced by global bounding main circulation: estimating the uncertainty. J Geophys Res Oceans. https://doi.org/10.1002/2016/C011633
-
Irrgang C, Saynisch J, Thomas One thousand (2016b) Touch on of variable seawater conductivity on motional induction simulated with an ocean full general circulation model. Body of water Sci 12(1):129–136
-
Knudsen M, Forch C, Sorensen S (1902) Bericht uber die chemische und physikalische Untersuchung des Seewassers und dice Aufstellung der neuen hydrographischen Tabellen, Kommission zur wissenschaftlichen Untersuchung der deutschen Meere
-
Kuvshinov A (2008) 3-D global induction in the oceans and solid earth: recent progress in modeling magnetic and electrical fields from sources of magnetospheric, ionospheric and oceanic origin. Surv Geophys 29(2):139–186
-
Kuvshinov A, Junge A, Utada H (2006) 3-D modelling the electrical field due to bounding main tidal flow and comparison with observations. Geophys Res Lett 33(6):L06314 (239–241)
-
Manoj C, Kuvshinov A, Maus S, Luhr H (2006) Sea apportionment generated magnetic signals. World Planets Space 58(4):429–437. https://doi.org/10.1186/BF03351939
-
McDougal TJ, Barker PM (2011) Getting started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox, SCOR/IAPSO WG127. ISBN 978-0-646-55621-five
-
Olsen N, Lühr H, Sabaka TJ, Mandea G, Rother M, Tøffner-Clausen L, Choi Due south (2006) Anarchy—a model of the Earth'south magnetic field derived from Champ, Ørsted, and SAC-C magnetic satellite data. Geophys J Int 166(1):67–75
-
Sabaka TJ, Olsen North, Tyler RH, Kuvshinov A (2015) CM5, a pre-Swarm comprehensive geomagnetic field model derived from over 12 year of Champ, Orsted, SAC-C and observatory information. Geophys J Int 200(3):1596–1626
-
Sabaka TJ, Tyler RH, Olsen N (2016) Extracting ocean-generated tidal magnetic signals from swarm data through satellite gradiometry. Geophys Res Lett 43:3237–3245
-
Schnepf NR, Kuvshinov A (2015) Can we probe the electrical conductivity of the lithosphere and upper mantle using satellite tidal magnetic signals? Geophys Res Lett 42:3233–3239
-
Schnepf NR, Manoj C, Kuvshinov A, Toh H, Maus S (2014) Tidal signals in bounding main-bottom magnetic measurements of the Northwestern Pacific: ascertainment versus prediction. Geophys J Int 198(ii):1096–1110
-
Szuts ZB (2012) Using motionally-induced electric signals to indirectly mensurate ocean velocity: instrumental and theoretical developments. Prog Oceanogr 96(1):108–127
-
Tyler RH, Sanford TB, Oberhuber JM (1997) Geophysical challenges in using large-scale ocean-generated EM fields to determine the ocean flow. J Geomagn Geoelectr 49(11–12):1351–1372
-
Tyler RH, Maus S, Lühr H (2003) Satellite observations of magnetic fields due to ocean tidal menses. Scientific discipline 299(5604):239–241
-
Zweng MM, Reagan JR, Antonov JI, Locarnini RA, Mishonov AV, Boyer TP, Garcia HE, Baranova OK, Johnson DR, Seidov D, Biddle MM (2013) World Ocean Atlas 2013. In: Levitus S, Mishonov A (eds) Tech. Ed. NOAA Atlas NESDIS, vol ii: Salinity, vol 74
Authors' contributions
All authors contributed to the pattern, implementation, and writing of this report, with the following leading tasks: RHT was involved in conception/pattern of written report, analyses of gridded data, and writing; TPB was involved in pattern and objective analyses of observations; TM was involved in description and implementation of TEOS conversion formulae; MMZ was involved in quality control of data; JRR was involved in quality control and generation of supporting material comparing study. All authors read and approved the final manuscript.
Acknowledgements
RHT acknowledges support from the NASA Earth Surfaces and Interiors Programme. This study was partially supported by NOAA grant NA14NES4320003 (Cooperative Plant for Climate and Satellites—CICS) at the University of Maryland/ESSIC. Additional back up was provided by the Ocean Observing and Monitoring Division, Climate Program Office, National Oceanic and Atmospheric Assistants, U.S. Department of Commerce. The authors wish to thank Trevor McDougall for helpful discussions.
Competing interests
The authors declare that they have no competing interests.
Availability of data and materials
The conductivity climatological information presented here are bachelor at http://www.nodc.noaa.gov/OC5/woa13/.
Consent for publication
Not applicable.
Ethics approval and consent to participate
Non applicable.
Funding
Funding support for this piece of work includes the NASA Earth Surface and Interiors Program, the Japan Social club for the Promotion of Science, and NOAA.
Publisher's Annotation
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Affiliations
Corresponding author
Additional file
40623_2017_739_MOESM1_ESM.pdf
Additional file i: Figure S1. Depth-averaged conductivity anomaly (relative to annual hateful) for each of the four seasons. The full range in the data are, respectively, −0.660–−0.556 (S/m), −0.471–−0.317 (South/k), −0.511–−0.721 (S/thousand), −0.502–−0.594 (S/one thousand).
40623_2017_739_MOESM2_ESM.docx
Additional file 2. Supplement certificate comparison results here with results from a previous study.
40623_2017_739_MOESM3_ESM.avi
Boosted file three. Film of ocean conductivity showing frames moving from surface to ocean floor.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/four.0/), which permits unrestricted use, distribution, and reproduction in whatsoever medium, provided you lot give advisable credit to the original author(s) and the source, provide a link to the Artistic Commons license, and indicate if changes were made.
Reprints and Permissions
About this article
Cite this article
Tyler, R.H., Boyer, T.P., Minami, T. et al. Electrical conductivity of the global ocean. Earth Planets Space 69, 156 (2017). https://doi.org/10.1186/s40623-017-0739-7
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/10.1186/s40623-017-0739-7
Keywords
- Electrical electrical conductivity
- Conductance
- Ocean
- Climatology
Source: https://earth-planets-space.springeropen.com/articles/10.1186/s40623-017-0739-7
0 Response to "The Latter Again Is More Conductive to the Former What Does This Mean"
Post a Comment